混叠

　　我们看电影时，如果里面有汽车启动时的镜头，会看到轮子显示越转越快，然后在某个时刻突然看起来变慢，甚至反转。这是因为电影摄影机相当于一个固定的频率Fs对连续的车轮采样，当车轮转速超过Fs/2并继续提高时，看到的就是混叠干扰下的结果。

　　奈奎斯特采样定理规定要使连续信号采样后能够不失真还原，采样频率必须大于信号最高频率的两倍(即奈奎斯特频率)。当采样频率Fs低于奈奎斯特频率时，重构的连续信号中原信号F/2以上的频率会对称的映象到了F/2以下的频带中，并且和F/2以下的原有频率成分叠加起来。

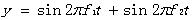
　　对我们以三种不同的频率对这个函数进行采样，分别得出欠采样、临界采样、过采样的频谱，从三张频谱中我们分析三种采样与混叠的关系。

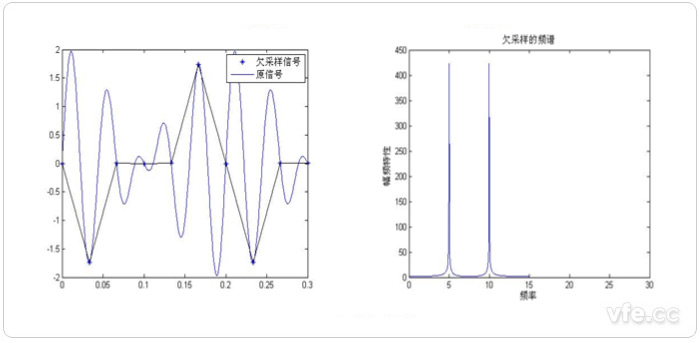
　　图示1：欠采样频谱分析示意图

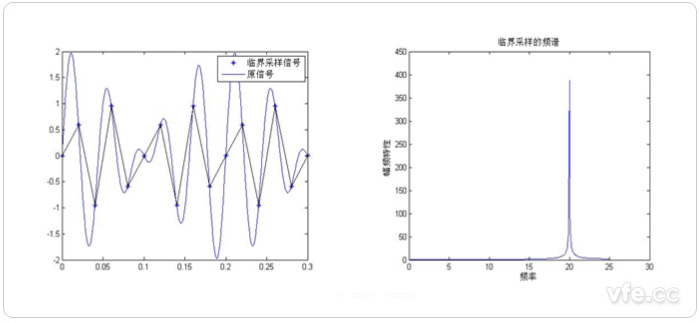
　　图示2：临界采样频谱分析示意图

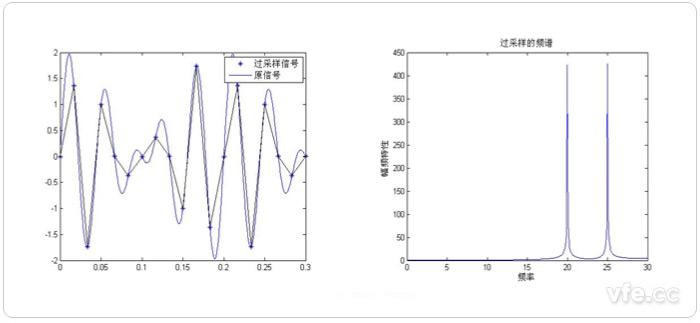
　　图示3：过采样频谱分析示意图

　　由图示三种采样频率后的频谱分析可知：欠采样(FS<2F)会产生频谱混叠；临界采样(FS=2F)也会产生混叠现象；过采样(FS>2F)不会产生混叠现象。

　　混叠是数字信号处理中的一个重要概念，它是数字信号处理中的特有现象，是数字信号中离散采样引起的。混叠现象会产生假频率、假信号、会严重的影响测量结果，当采样频率小于模拟信号中所要分析的最高分量的频率的2倍，就会发生。因此，我们通常采用以下两种手段来消除混叠现象，保证测量精度。

　　1、 提高采样频率，使之达到被测信号最高频率的两倍以上；

　　2、 引入低通滤波器或提高低通滤波器的参数(该低通滤波器通常称为抗混叠滤波器)，抗混叠滤波器可限制信号的带宽，使之满足采样定理的条件。