干扰可以提高测量精度,是真的吗?
- 浏览次数:9459次
- 发布时间:2013/11/26 18:06:28
- 作者:银河电气
一、前言
水可以引燃蜡烛,是真的吗?是真的!
蛇怕雄黄,是真的吗?是假的!
上述两个现象,已经由央视 财经频道《是真的吗?》揭秘。
今天要探讨的是:
干扰可以提高测量精度,是真的吗?
通常情况下,干扰是测量的天敌,干扰会降低测量精度,严重情况会导致测量不能正常进行,就这个角度而言,干扰可以提高测量精度,是假的!
然而,是否总是如此呢?是否存在一种情况,干扰不但不会降低测量精度,反而会提高测量精度呢?
答案是肯定的!
二、干扰的约定
结合实际情况,我们对干扰进行如下约定:
1、干扰不含直流分量。实际测量中,干扰主要为交流干扰,这个假设是合理的。
2、干扰与被测直流电压相比,幅值相对较小。这一点符合实际情况。
3、干扰是周期信号,或固定一段时间内均值为零。这一点,实际测量中不一定成立。但是,由于干扰一般为较高频率的交流信号,对于多数干扰而言,在较长的时间段内,均值为零的约定是合理的。
三、干扰下的测量精度
现在电测量仪器仪表大多采用AD转换器,其测量精度与AD转换器的分辨力密切相关,一般而言,较高分辨力的AD转换器具有较高的测量精度。
然而,AD分辨力总是有限的,假设AD的分辨率为3位,最高测量电压为8V,AD转换器就相当于一把等分为8格,每格为1V的刻度尺,AD分辨力为1V。该AD的测量结果总为整数,而小数部分总是被进位或舍弃,本文假设为进位。进位或舍弃会引起测量误差,例如,6.3V大于6V,小于7V,AD测量结果为7V,存在0.7V的误差,我们称这个误差为AD量化误差。
为了分析方便,我们假设刻度尺(AD转换器)除了AD量化误差之外,不存在其它的测量误差。
现在,我们用这样的两把相同的刻度尺来测量图1所示的无干扰(理想情况)的和有干扰的两个直流电压。
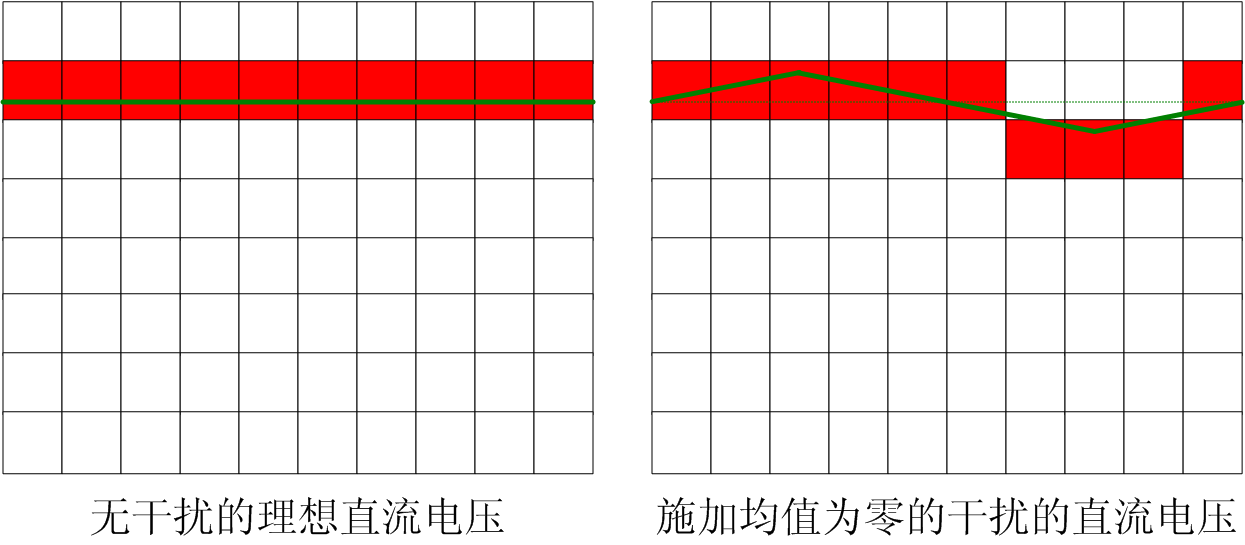
如图1所示,实际被测直流电压为6.3V,左图直流电压没有任何的干扰,数值上为恒定值。右图为受到交流干扰的直流电,数值上有一定的波动。右图直流电剔除干扰信号之后与左图直流电电压相等。图中红色方块表示AD转换器的转换结果。
图1 无干扰的直流电和受交流干扰的直流电压
对上图中两种情况下的直流电分别进行10次测量,再对10次测量结果求平均。
左图第一把刻度尺测量10次,每次读数相同,受
AD量化误差的影响,每次读数均为7V,10次测量求平均后,结果还是7V,AD量化误差为0.7V,测量误差为0.7V。
右图第二把刻度尺发生了戏剧性的变化:
因干扰电压的正负及幅值的不同,不同测量点上AD量化误差不同,在AD量化误差的变化下,AD测量结果在6V和7V之间变化。其中有7次测量结果为7V,只有三次测量结果为6V,10次测量结果的均值为6.3V!误差为0V!
实际上,无误差是不可能的,因为客观世界中,不存在严格的6.3V!但是,的的确确存在的是:
无干扰的情况下,由于每次测量结果相同,10次测量求平均后,误差不变!
而存在适量干扰时,10次测量求平均后,AD量化误差减小了一个数量级!分辨力提高了一个数量级!测量精度也提高了一个数量级!
关键问题是:
被测电压为其它数值时,是否也是如此呢?
读者不妨自己按照第二节对干扰的约定,用系列数值表示干扰,将干扰叠加到被测电压上,再按照AD转换器的进位原则,计算各个点的测量结果,再求均值进行验证,只要干扰幅值能够引起AD量化后的读数变化,且采样频率足够高(干扰幅值变化有过渡过程,而不是正负相间的两个数值),精度一定提高!
可以证明,只要被测电压不是正好为整数(客观世界中是不存在的),都会存在AD量化误差,而不论AD量化误差为多大,只要干扰的幅值大于AD量化误差或大于AD的最小分辨力,就会导致测量结果在相邻两个数值之间变化。由于干扰是正负对称的,减小和增大的幅度和概率是相等的,因此,当实际值较靠近哪个数值,哪个数值出现的概率就大,平均后就会靠近哪个数值。
即:多次测量的均值(干扰均值为零)必然更加接近无干扰时的测量结果,也就是说,利用均值为零的交流干扰信号,采用多次测量求平均,可以减小等效的AD量化误差,提高AD测量分辨力,提高测量精度!
干扰可以提高测量精度,是真的吗?
扩展阅读:
分享知识、传递科学,原创文章,欢迎转载,转载请注明出处:
作者:AnyWay中国