一脉冲信号的上升时间简介

　　脉冲信号的上升时间是指脉冲瞬时值最初到达规定下限和规定上限的两瞬时之间的间隔，除另有规定外，下限和上限分别定义为脉冲峰值幅度的10%和90%。在控制领域中，上升时间是指响应曲线从零时刻到首次达到稳态值的时间，通常定义为响应曲线从稳态值的10%上升到稳态值的90%所需的时间。

　　很多信号完整性问题都是由信号上升时间短引起的，那么信号上升时间和信号带宽有什么关系呢？

　　对于数字电路，输出的通常是方波信号，方波的上升边沿非常陡峭，根据傅里叶分析，任何信号都可以分解成一系列不同频率的正弦信号，方波中包含了非常丰富的频谱成分。

　　抛开枯燥的理论分析，我们用实验来直观的分析方波中的频率成分，看看不同频率的正弦信号是如何叠加成为方波的。

二信号上升时间与带宽的关系

　　首先我们把一个1.65V的直流和一个100MHz的正弦波形叠加，得到一个直流偏置为1.65V的单频正弦波。我们给这一信号叠加整数倍频率的正弦信号，也就是通常所说的谐波。

　　3次谐波的频率为300MHz，5次谐波的频率为500MHz，以此类推，高次谐波都是100MHz的整数倍。

　　图1是叠加不同谐波前后的比较，左上角的是直流偏置的100MHz基频波形，右上角是基频叠加了3次谐波后的波形，有点类似方波了，左下角是基频+3次谐波+5次谐波的波形，右下角是基频+3次谐波+5次谐波+7次谐波的波形。这里可以直观的看到叠加的谐波成分越多，波形就越像方波。

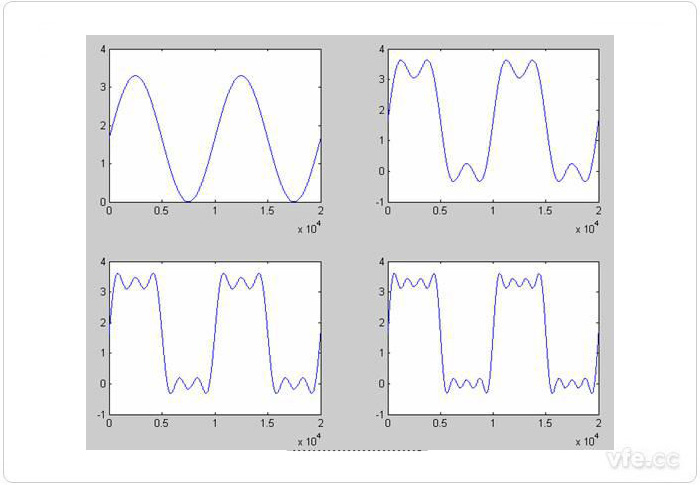
图1 叠加不同谐波前后比较

　　因此如果叠加足够多的谐波，我们就可以近似的合成方波，图2是叠加到217次谐波后的波形，已经非常近似方波了，不用关心角上的那些毛刺，那是著名的吉伯斯现象，不影响对问题的理解。

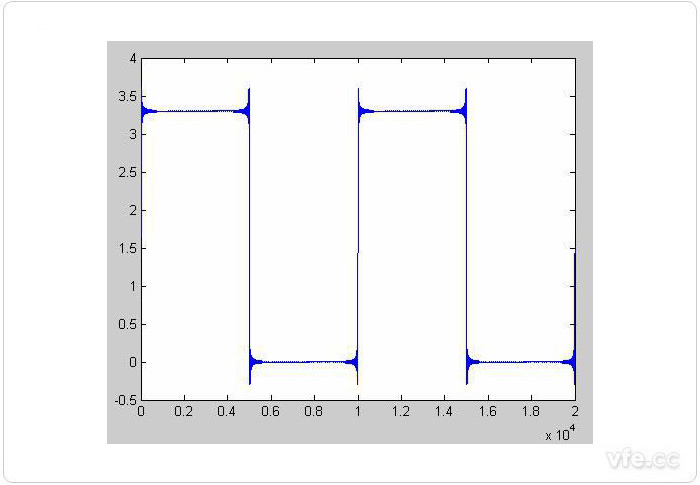
图2 叠加217次谐波后的波形

　　上面的实验非常有助于我们理解方波波形的本质特征，理想的方波信号包含了无穷多的谐波分量，可以说带宽是无限的。实际中的方波信号与理想方波信号有差距，但是有一点是共同的，就是所包含频率很高的频谱成分。

　　现在我们看看叠加不同频谱成分对上升沿的影响。图3是对比显示，蓝色是基频信号上升边沿，绿色是叠加了3次谐波后的波形的上升边沿，红色是基频+3次谐波+5次谐波+7次谐波后的上升边沿，黑色是一直叠加到217次谐波后的波形上升边沿。

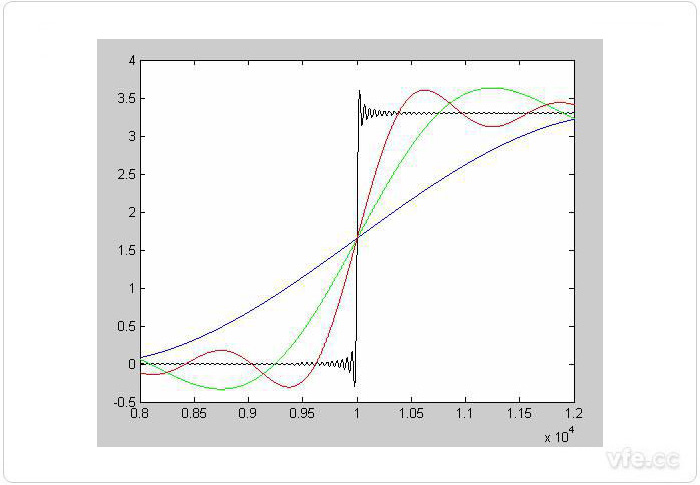
图3 叠加不同谐波后的波形上升边沿比较

　　通过图3我们可以看到，谐波分量越多，上升沿越陡峭。或从另一个角度说，如果信号的上升边沿很陡峭，上升时间很短，那该信号的带宽就很宽。上升时间越短，信号的带宽越宽。

三结论

　　这里说一下，最终合成的方波，其波形重复频率就是100MHz。叠加谐波只是改变了信号上升时间。信号上升时间和100MHz这个频率无关，换成50MHz也是同样的规律。如果你的电路板输出数据信号只是几十MHz，你可能会不在意信号完整性问题。但这时你想想信号由于上升时间很短，频谱中的那些高频谐波会有什么影响？记住一个重要的结论：影响信号完整性的不是波形的重复频率，而是信号的上升时间。

---